MATEMATICA E CIVILTÀ: UNA CRISI EPOCALE. Odifreddi dà alla matematica l’onore di grande motore della civiltà, ma ancora non sa «Che cos’è il numero, che l’uomo lo può capire? E che cos’è l’uomo, che può capire il numero?». La sua recensione di un saggio di Alex Bellos, con alcune note - di Federico La Sala
- [...] stupisce quindi che il libro di Bellos sia in realtà una storia delle civiltà mascherata, osservata e raccontata dai complementari punti di vista del numero, delle cifre e del calcolo: tre aspetti di un’unica realtà, che costituiscono le versioni aritmetiche del pensiero, della scrittura e del linguaggio. Né stupisce che il libro mostri che, come le idee sono legate alla lingua in cui vengono espresse, e le parole sono legate alla scrittura con cui vengono registrate, così le varie civiltà abbiano affrontato e risolto in maniera diversa i problemi di definire filosoficamente i numeri, rappresentarli semioticamente e manipolarli matematicamente, rispondendo in maniera diversa alla domande su che cosa essi siano, come si possano indicare e come li si possa maneggiare [...]
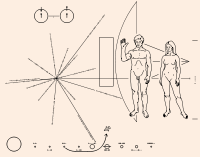
- FOTO: Immagine della placca del Pioneer 10.
È la matematica il grande motore della civiltà
Il sistema oggi in vigore in Occidente è stato "inventato" in India nel V secolo e poi tramandato dagli arabi agli europei
 Risultati geometrici, astronomici e architettonici molto importanti sono stati raggiunti da vari popoli in epoche e luoghi diversi
Risultati geometrici, astronomici e architettonici molto importanti sono stati raggiunti da vari popoli in epoche e luoghi diversi
 Un saggio di Bellos mostra come, dall’abaco alle tabelline, lo sviluppo dell’uomo sia legato al saper contare
Un saggio di Bellos mostra come, dall’abaco alle tabelline, lo sviluppo dell’uomo sia legato al saper contare
di Piergiorgio Odifreddi (la Repubblica, 23.02.2011)
Se avesse voluto apporre un’epigrafe al suo libro Il meraviglioso mondo dei numeri (pubblicato da Einaudi Stile Libero), Alex Bellos avrebbe potuto usare la duplice domanda del neurofisiologo Warren McCulloch: «Che cos’è il numero, che l’uomo lo può capire? E che cos’è l’uomo, che può capire il numero?». Perché il suo sterminato ed enciclopedico libro è appunto un tentativo, divertente e riuscito, di rispondere a entrambi gli interrogativi, e di mostrare come le storie del numero e dell’uomo siano in realtà intrecciate in maniera inestricabile, e i progressi e regressi dell’uno siano andati di pari passo coi progressi e regressi dell’altro.
L’espressione "mondo dei numeri" del titolo si riferisce dunque non soltanto al concetto oggettivo di numero da una parte, e alle sue rappresentazioni soggettive nello spazio geografico e nel tempo storico dall’altra, ma anche alle facoltà intellettuali dell’uomo. In particolare, al fatto che la scrittura alfabetica e la notazione numerica hanno sempre fecondamente intessuto, in teoria e in pratica, un rapporto di mutua stimolazione e derivazione.
Non stupisce quindi che il libro di Bellos sia in realtà una storia delle civiltà mascherata, osservata e raccontata dai complementari punti di vista del numero, delle cifre e del calcolo: tre aspetti di un’unica realtà, che costituiscono le versioni aritmetiche del pensiero, della scrittura e del linguaggio. Né stupisce che il libro mostri che, come le idee sono legate alla lingua in cui vengono espresse, e le parole sono legate alla scrittura con cui vengono registrate, così le varie civiltà abbiano affrontato e risolto in maniera diversa i problemi di definire filosoficamente i numeri, rappresentarli semioticamente e manipolarli matematicamente, rispondendo in maniera diversa alla domande su che cosa essi siano, come si possano indicare e come li si possa maneggiare.
Naturalmente, non tutte le civiltà hanno trovato "la soluzione" di questi problemi, che consiste in una ricetta che combina i seguenti quattro ingredienti. -Primo, scegliere una base arbitraria ma conveniente: ad esempio, dieci.
 Secondo, indicare tutti i numeri positivi minori della base con segni differenti: ad esempio, le cifre da 1 a 9.
Secondo, indicare tutti i numeri positivi minori della base con segni differenti: ad esempio, le cifre da 1 a 9.
 Terzo, rappresentare i numeri maggiori mediante un sistema posizionale, in cui le cifre hanno un valore diverso a seconda di dove si trovano: ad esempio, assegnando allo stesso 1 il valore di uno, dieci o cento, e allo stesso 2 il valore di due o venti, nelle espressioni 1, 12 e 123).
Terzo, rappresentare i numeri maggiori mediante un sistema posizionale, in cui le cifre hanno un valore diverso a seconda di dove si trovano: ad esempio, assegnando allo stesso 1 il valore di uno, dieci o cento, e allo stesso 2 il valore di due o venti, nelle espressioni 1, 12 e 123).
 E quarto, aggiungere una cifra (ad esempio, 0) per rappresentare allo stesso tempo sia un posto vuoto nella precedente rappresentazione, sia il numero zero corrispondente a una quantità nulla.
E quarto, aggiungere una cifra (ad esempio, 0) per rappresentare allo stesso tempo sia un posto vuoto nella precedente rappresentazione, sia il numero zero corrispondente a una quantità nulla.
Anzi, questa "soluzione" è il lascito culturale all’umanità di un’unica, grande civiltà: quella indiana della dinastia Gupta, che regnò nella valle del Gange e dei suoi affluenti tra il terzo e il sesto secolo della nostra era, ed è ricordata anche nella storia dell’arte per i suoi capolavori, primi fra tutti le pitture e le sculture delle grotte di Ajanta. La più antica registrazione dell’uso del sistema numerico indiano viene dalla Lokavibhaga: un’opera del 458, la cui datazione stabilisce un limite temporale superiore alla nascita del sistema numerico che oggi è universalmente in vigore nel mondo intero, dopo essere stato adottato dagli Arabi, e da essi tramandato agli Europei.
I quali, come ricorda Bellos, non soltanto l’hanno accettato con grandi e secolari resistenze, ma ancor oggi lo usano in maniera impropria. Ad esempio, privilegiando alcune potenze della base dieci come il mille, il milione o il miliardo, e non assegnando alle potenze intermedie nomi propri, bensì nomi composti come diecimila e centomila, o dieci milioni e cento milioni, che trattano quelle potenze come basi aggiuntive al dieci e macchiano la purezza del relativo sistema decimale. Una stonatura che invece gli indiani seppero evitare.
Come racconta Bellos, il massimo numero per il quale gli indiani coniarono un nome fu quello delle gocce di pioggia che potrebbero cadere in diecimila anni sull’insieme dei mondi, valutato dal Buddha in dieci alla centoquaranta e da lui chiamato asankhya: una parola sanscrita che significa letteralmente "innumerabile" o "incalcolabile". In Occidente soltanto Archimede poté competere con queste imprese: per rimediare alla pochezza della lingua greca, che aveva come massimo nome di numero la miriade, pari a diecimila, nell’Arenario egli inventò un modo sistematico per parlare di grandi numeri e lo applicò al calcolo del numero dei granelli di sabbia che potevano riempire l’universo, da lui valutato in dieci alla sessantatrè.
Ma non solo i Greci non avevano nomi per i grandi numeri: non avevano neppure le cifre, e usavano le lettere al loro posto. Poiché l’alfabeto classico aveva ventiquattro lettere, aggiungendone tre cadute in disuso essi ottennero un sistema di ventisette lettere, che divisero in tre gruppi di nove ciascuno: le prime nove per le unità, le seconde nove per le decine, e le ultime nove per le centinaia. Questo permise divertimenti come la composizione di poemi isopsefi, "a stesso calcolo", in cui tutti i versi avevano la stessa somma numerica delle lettere. O paranoie come la lettura simbolica di numeri quali l’apocalittico 666, variamente interpretato nei secoli come il nome di Nerone, Diocleziano, Lutero o il Papa.
Ma non facilitò le operazioni aritmetiche, per le quali si dovette ricorrere a vari tipi di abaco: una letterale "tavoletta" che poteva essere di sabbia, di cera o a gettoni, e che permetteva di compiere in maniera analogica le operazioni che il sistema indiano permette invece di fare sulla carta in maniera digitale, manipolando le cifre con l’ausilio delle "tabelline’’. Bellos ci narra che l’abaco fu usato, in qualche forma, da tutti i popoli che non possedettero un adeguato sistema numerico che permettesse di fare i "calcoli": una parola, questa, che significa letteralmente "pietruzza" (come nel caso dei calcoli al fegato o alla cistifellea), e richiama l’origine primordiale dei numeri.
È in queste molteplici origini che si trovano le tante albe del numero di cui trattano i vari capitoli del libro di Bellos. Il sistema sessagesimale additivo dei Sumeri, ad esempio, di cui rimangono vestigia nel nostro computo dei secondi in un minuto, dei minuti in un’ora e dei gradi in un angolo giro. Il sistema decimale posizionale dei Babilonesi, che introdusse lo zero come posto vuoto. Il sistema vigesimale posizionale dei Maya, che arrivò a considerare lo zero come numero indipendente. E soprattutto il sistema completo di tutti gli ingredienti degli Indiani, che condividono con i Babilonesi, i Cinesi e i Maya l’introduzione del sistema posizionale, con i soli Maya l’invenzione dello zero, ma con nessun altro l’intuizione della necessità di indicare in maniera indipendente tutti i numeri minori della base.
Analogamente all’evoluzione biologica dell’uomo, o all’evoluzione linguistica dell’alfabeto, non bisogna però guardare all’evoluzione numerica del sistema indiano come a una teleologia. Da un lato, infatti, la constatazione che solo una civiltà è arrivata alla "soluzione" mostra che quest’ultima non può essere vista come un’inevitabile necessità, e dev’essere piuttosto considerata come una fortunata contingenza. E, dall’altro lato, i risultati geometrici, astronomici e architettonici raggiunti rispettivamente dai Greci, dai Maya e dai Romani, che possedevano solo sistemi numerici parziali e incompleti, mostrano che il progresso matematico, scientifico e tecnologico può evolversi in direzioni multiple e complementari, di molte delle quali Il meraviglioso mondo dei numeri narra le affascinanti vicende.
SUL TEMA, NEL SITO, SI CFR.:
 UNITÀ D’ITALIA E FOLLIA: EMERGENZA LOGICO-MATEMATICA EPOCALE. PER UN CONVEGNO E UNA RIFLESSIONE SUL CONCETTO DI ’UNITÀ’ E DI SOVRANITÀ (SOVRA-UNITÀ). Materiali sul tema
UNITÀ D’ITALIA E FOLLIA: EMERGENZA LOGICO-MATEMATICA EPOCALE. PER UN CONVEGNO E UNA RIFLESSIONE SUL CONCETTO DI ’UNITÀ’ E DI SOVRANITÀ (SOVRA-UNITÀ). Materiali sul tema
 SAPERE AUDE!: USCIRE DALLA CAVERNA, USCIRE DALLO STATO DI MINORITÀ, USCIRE DALLA "PREISTORIA" E NON RICADERE NELL’ILLUSIONE E NEL DELIRIO DELL’ “UOMO SUPREMO” DEI VISIONARI E DEI METAFISICI ATEI-DEVOTI
SAPERE AUDE!: USCIRE DALLA CAVERNA, USCIRE DALLO STATO DI MINORITÀ, USCIRE DALLA "PREISTORIA" E NON RICADERE NELL’ILLUSIONE E NEL DELIRIO DELL’ “UOMO SUPREMO” DEI VISIONARI E DEI METAFISICI ATEI-DEVOTI
Forum
-
> MATEMATICA E CIVILTÀ: UNA CRISI EPOCALE. --- LA "LOGICA" DEL "MENTITORE" (DEL "VENDITORE" E DEL "BANDITO"). Il dizionario della stupidità di Odifreddi (di Marco Grimaldi)9 ottobre 2016, di Federico La Sala
- COSTITUZIONE E PENSIERO. ITALIA: LA MISERIA DELLA FILOSOFIA ITALIANA E LA RICCHEZZA DEL MENTITORE ISTITUZIONALIZZATO ...
 BERTRAND RUSSELL: LA LEZIONE SUL MENTITORE (IGNORATA E ’SNOBBATA’), E "L’ALFABETO DEL BUON CITTADINO".
BERTRAND RUSSELL: LA LEZIONE SUL MENTITORE (IGNORATA E ’SNOBBATA’), E "L’ALFABETO DEL BUON CITTADINO".
Il dizionario della stupidità di Odifreddi
di Marco Grimaldi (Le Parole e le Cose, 9 ottobre 2016)
Su Dante e Odifreddi ho già scritto qualche tempo fa (e non so se almeno uno dei due gradirebbe ritrovare così spesso il proprio nome accanto a quello dell’altro). Ma Odifreddi è recidivo e ammette difficilmente di avere torto. Oppure si riscrive senza pensarci troppo. O ha un ghost writer che lo riscrive di continuo. Nel Dizionario della stupidità appena pubblicato da Rizzoli (sottotitolo: Fenomenologia del non-senso della vita), alla voce Dante, si legge infatti (p. 79):
- Nel Trattatello in laude di Dante (1360 circa) il Boccaccio racconta che, quando il poeta morì, la Commedia era incompiuta. Mancavano gli ultimi tredici canti, e i figli Iacopo e Pietro furono convinti dagli amici a completarla. Otto mesi dopo la morte il padre apparve però al primo in sogno, lo condusse per mano in una camera e gli indicò una stuoia sul muro, sotto la quale il giorno dopo furono miracolosamente ritrovati gli ammuffiti canti mancanti.
 Che cos’è più stupido pensare? Che i figli abbiano completato l’incompiuta opera del padre? O che egli avesse nascosto gli ultimi canti, invece di spedirli a Cangrande della Scala come faceva regolarmente man mano che li finiva, e che essi siano stati ritrovati in seguito a un sogno?
Che cos’è più stupido pensare? Che i figli abbiano completato l’incompiuta opera del padre? O che egli avesse nascosto gli ultimi canti, invece di spedirli a Cangrande della Scala come faceva regolarmente man mano che li finiva, e che essi siano stati ritrovati in seguito a un sogno?
 Anche per il Deuteronomio si è stupidamente sostenuto per due millenni che fosse opera di Mosè, ma poi si è dovuto ammettere che invece l’aveva scritto Giosia, inventando il ritrovamento di un perduto rotolo della Torah. E anche noi oggi facciamo spesso i veri o i finti tonti, credendo o fingendo di credere che un autore famoso abbia lasciato una quantità sospetta di opere postume, che sono ovviamente state scritte da altri: spesso, gli stessi che comunque gliele scrivevano già da vivi.
Anche per il Deuteronomio si è stupidamente sostenuto per due millenni che fosse opera di Mosè, ma poi si è dovuto ammettere che invece l’aveva scritto Giosia, inventando il ritrovamento di un perduto rotolo della Torah. E anche noi oggi facciamo spesso i veri o i finti tonti, credendo o fingendo di credere che un autore famoso abbia lasciato una quantità sospetta di opere postume, che sono ovviamente state scritte da altri: spesso, gli stessi che comunque gliele scrivevano già da vivi.
In questa paginetta Odifreddi condensa una tesi già esposta in Il giro del mondo in 80 pensieri (Rizzoli, 2015, pp. 285-89): Dante non ha scritto gli ultimi canti della Commedia; li hanno scritti i figli e hanno finto di averli ritrovati per non guastare il brand “Dante” che già allora si rivelava redditizio.
In Il giro del mondo Odifreddi se la prendeva con il poeta: dato che gli ultimi canti non li ha neanche scritti lui, perché continuare a leggerlo a scuola? Meglio passare a Newton e Galileo che almeno ci insegnano il pensiero scientifico. Nel Dizionario se la prende con gli stupidi, cioè quelli che non accettano la sua tesi. La domanda è quindi retorica: secondo Odifreddi è stupido pensare «che egli avesse nascosto gli ultimi canti [...], e che essi siano stati ritrovati in seguito a un sogno», proprio come è stupido pensare che il Deuteronomio l’abbia scritto Mosè. E a rigor di logica Odifreddi, che logico è, avrebbe anche ragione.
Il problema - che è poi un problema classico dell’applicazione della logica astratta alla realtà concreta - è che quelle non sono le due sole risposte possibili. Prima di tutto Boccaccio, che è l’unico appiglio per la tesi di Odifreddi, non è una fonte totalmente affidabile. La storia del ritrovamento in sogno non è per forza vera ed è difficile capire perché Boccaccio la riferisca: forse semplicemente perché era una bella storia che aveva sentito in giro.
La cosa più stupida da pensare è che si debba scegliere tra quelle due alternative; è infatti molto meno stupido ritenere che il racconto sia stato inventato da Boccaccio o dalla sua fonte e che Dante abbia davvero concluso la Commedia, dato che gli ultimi canti sono perfettamente integrati e coerenti con il resto dell’opera. E che i suoi figli, che quando scrivono in versi sono poeti infinitamente meno bravi del padre, non abbiano avuto alcun ruolo nella sua realizzazione, mentre sappiamo con certezza che ne hanno avuto uno, fondamentale, nella divulgazione e nell’opera di interpretazione del poema.
Tuttavia, la Commedia non è l’unica cosa che conta: il vero motivo per cui vale la pena preoccuparsi dell’opinione di Odifreddi su Dante è che questo Dizionario della stupidità, assieme a gran parte dei suoi libri recenti, è un buon esempio di cattiva divulgazione. E sarebbe fin troppo facile sostenere che Odifreddi faccia cattiva divulgazione perché è stupido a sua volta.
Ma che cos’è uno stupido? Secondo Carlo Maria Cipolla, che ha scritto un famoso libretto intitolato Le leggi fondamentali della stupidità umana, lo stupido è chi causa un danno ad un’altra persona o gruppo di persone senza nel contempo realizzare alcun vantaggio per sé o addirittura subendo una perdita.
Odifreddi trae certamente un vantaggio scrivendo dei libri che qualche copia dovranno pur venderla se Rizzoli continua a stamparglieli. Quindi non è uno stupido (anche se qualche tempo fa si è fatto fregare dalla Zanzara). Cipolla identificava però altre tre categorie, disponendole assieme allo Stupido su un diagramma: lo Sprovveduto, l’Intelligente e il Bandito. L’idea era che non esistano né uomini perfettamente stupidi, sprovveduti o intelligenti né dei perfetti banditi, ma che le categorie siano fluide e la realtà sia più complessa. Ciò non toglie che ciascuno di noi tende ad assomigliare più all’una che all’altra categoria.
Se Odifreddi non è uno stupido, non è neanche uno Sprovveduto, che per Cipolla è chi compie un’azione e ne ricava una perdita mentre nello stesso tempo procura un vantaggio a qualcun altro. Restano l’Intelligente e il Bandito. Il primo è chi compie un’azione dalla quale ottiene un vantaggio e nello stesso tempo procura un vantaggio anche a qualcun altro.
Odifreddi vende e Rizzoli ne trae vantaggio: se tutto finisse lì, potremmo classificarlo tra gli intelligenti. Ma il fatto è che Odifreddi, oltre a creare un vantaggio per sé e per il suo editore (e forse si possono far coincidere questi due interessi), allo stesso tempo danneggia qualcun altro. Questo qualcun altro sono tutti quelli che in varie sedi - a scuola, all’università, in televisione, sui giornali - cercano di parlare di cose serie come Dante, Galileo e Darwin in modo semplice ed esatto, ma sono soprattutto i lettori di Odifreddi, i quali credendo di trovare nel Dizionario della stupidità un elenco di cose stupide delle quali ridere, trovano un catalogo di stupidaggini nelle quali rischiano di credere. E questa (chi compie un’azione dalla quale trae vantaggio causando una perdita a qualcun altro) è la definizione del Bandito.
- COSTITUZIONE E PENSIERO. ITALIA: LA MISERIA DELLA FILOSOFIA ITALIANA E LA RICCHEZZA DEL MENTITORE ISTITUZIONALIZZATO ...
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. ---IMPARARE A CONTARE!!! IL "DIZIONARIO DELLA STUPIDITA’" DI ODIFREDDI. Una intervista dell’HuffPost.25 settembre 2016, di Federico La Sala
COSTITUZIONE E PENSIERO. ITALIA: LA MISERIA DELLA FILOSOFIA ITALIANA E LA RICCHEZZA DEL MENTITORE ISTITUZIONALIZZATO ...
Piergiorgio Odifreddi, intervista Huffpost: "Il 90 per cento degli italiani è stupido"
- Beppe Grillo: "È un minus habens". I grillini: "Peggio di lui". In generale: "Il novanta per cento delle persone è stupido. In un paese di 60 milioni di abitanti come l’Italia, saranno all’incirca 54 milioni: non possono essere andati tutti alla festa nazionale dei 5 stelle a Palermo".
 Piergiorgio Odifreddi - matematico, divulgatore scientifico, saggista - ha scritto un Dizionario della stupidità (Rizzoli, 378 pagine, 18 euro) per proteggersi dalle "scemenze della vita quotidiana".
Piergiorgio Odifreddi - matematico, divulgatore scientifico, saggista - ha scritto un Dizionario della stupidità (Rizzoli, 378 pagine, 18 euro) per proteggersi dalle "scemenze della vita quotidiana".
 Laico fervente, ha studiato prima dalle suore, poi dai preti: "Non erano niente male". Se deve immaginare uno scenario politico peggiore di quello odierno, torna con la memoria alla stagione della Democrazia cristiana: "Anche se Giulio
Andreotti - racconta - mi salvò da un pericoloso fermo in Unione Sovietica".
Laico fervente, ha studiato prima dalle suore, poi dai preti: "Non erano niente male". Se deve immaginare uno scenario politico peggiore di quello odierno, torna con la memoria alla stagione della Democrazia cristiana: "Anche se Giulio
Andreotti - racconta - mi salvò da un pericoloso fermo in Unione Sovietica".
 Con l’Huffington Post, parla di banchieri da "mandare all’infermo", di politicamente corretto e Islam, della "superiorità" di Benedetto XVI sulla "banalità" di Papà Francesco, e di politica.
Con l’Huffington Post, parla di banchieri da "mandare all’infermo", di politicamente corretto e Islam, della "superiorità" di Benedetto XVI sulla "banalità" di Papà Francesco, e di politica.
di Redazione (l’Huffington post, 25/09/2016)
Odifreddi, nel suo dizionario c’è anche la voce: Matteo Renzi. Perché?
Se vogliono conquistare voti, i politici devono dire alle persone ciò che si vogliono sentir dire. Tendenzialmente, delle stupidaggini. E Matteo Renzi è l’erede perfetto di Berlusconi: il Cavaliere ha imparato a farlo cantando sulle navi, lui esordendo alla Ruota della fortuna.
Ma politicamente?
Renzi ha realizzato il programma berlusconiano, andando addirittura oltre con il Jobs act, che ha dissolto le tutele dello statuto dei lavoratori.
Dedica un lemma anche a Grillo.
Grillo ha iniziato a dire scemenze prima di cominciare a fare politica. Per dire: sosteneva che l’AIDS era una bufala, che l’OGM ammazza, che le radiazioni dei cellulari cuociono le uova. Ma lui ci crede. È questa la grande differenza tra Grillo e un politico di professione: che il politico deve dire delle cretinate per racimolare voti, lui le dice per convinzione.
Eppure ha un gran consenso.
Non voglio dire che il suo pubblico sia fatto di deficienti. È una parola brutta. Dico: ingenui. Ma rimane il fatto che sono persone che credono alle scie chimiche e fanno battaglie contro i detersivi. È la parte della società con meno mezzi culturali per giudicare.
Possibile che siano tutti così?
Bertrand Russell diceva che i politici hanno nei confronti degli elettori un vantaggio: che gli elettori sono più stupidi di loro. E giudicare Grillo, per me, è troppo difficile: mi è così distante che lo considero un minus habens. Quando lo sento, mi viene la pelle d’oca. Dicono che i suoi siano argomenti di pancia. Io fatico a considerarli proprio argomenti.
A Palermo, però, molte persone sono andate per ascoltarlo alla Festa nazionale dei 5 stelle.
Il novanta per cento delle persone è stupido. Quindi, considerato che siamo 60 milioni, in Italia ci sono almeno 54 milioni di stupidi: non credo ve ne siano di più a quella festa.
E gli altri dove vanno?
Vanno anche alle feste dell’Unità. Come si fa a pensare che dopo due anni di governo Renzi quella festa abbia un senso? Almeno, per decenza, cambiassero nome.
Non le sembra di sottovalutare? Il partito democratico governa il Paese, i Cinque stelle hanno conquistato due grandi città alle ultime elezioni.
C’è una differenza enorme tra le due città: a Torino, Chiara Appendino è il prodotto di ciò che i 5 stelle stessi chiamano poteri forti; a Roma, invece i poteri forti li hanno contro.
Può essere più esplicito?
Dietro Appendino c’è la Fiat. Appena aletta, John Elkan è subito corso a incontrarla. Viceversa, Virginia Raggi è dovuta recarsi in visita dal Papa.
C’è solo questa differenza tra le due?
No, Appendino ha le qualità per governare, Raggi le ha solo per vincere le elezioni.
Scrive: "E’ venuto il momento di tornare a considerare i banchieri paria della società e reietti da Dio".
Nel Medio Evo, era considerato usuraio chiunque prestasse denaro, a qualsiasi tasso. Oggi il fastidio per i banchieri è tornato a essere forte. Quando la gente vede i posti di lavoro che evaporano, le tutele che si dissolvono, e dall’altra gli aiuti di stato per tenere in vita istituti che hanno fallito, s’incazza.
Però è difficile vivere in un mondo senza banche.
Certo che si può vivere in un mondo senza banche. Per metà del secolo scorso, l’Unione Sovietica ne ha fatto a meno.
Non è andata benissimo, però.
Non per quel motivo. Mi domando perché non si possano nazionalizzare le banche che vengono salvate. Perché è diventata una bestemmia?
In Europa, nazionalizzare è contrario alle regole dell’Unione.
È per questo che l’UE suscita l’astio dei suoi cittadini: perché è solo un’unione economica.
Nel suo libro, mostra di preferire Ratzinger a Papa Francesco. Perché?
Da ateo, con Benedetto XVI ho avuto un dialogo. Mi è interessato leggere le cose che scriveva, Ratzinger aveva una profondità di pensiero. La statura intellettuale Papa Francesco lascia perplessi. Quando parla, mi cadono le braccia. La misericordia, il vogliamoci bene, l’amore: sono cose talmente banali. Chi può essere contrario?
È facile criticare l’Islam allo stesso modo in cui lei, ora, ha fatto con il Cattolicesimo?
Penso che, in realtà, sia molto più facile criticare l’islam che il Cristianesimo. Farlo, è politicamente corretto. Ci sono partiti politici che fanno propaganda sull’equazione musulmano uguale terrorista. E l’opinione pubblica è sempre sul chi va là.
Dimentica quello che è successo in Francia per le vignette di Charlie Hebdo su Maometto?
La diversità è che i cristiani non vengono sotto casa ad aspettarti se li prendi di mira con la satira. Ma ricorda la parodia di Ratzinger fatta da Crozza? A un certo punto ha dovuto smettere di farla. E potrei fare altri esempi. Nei risultati, non è molto diverso da quello che accade con l’Islam.
Lei è stato compagno di classe di Flavio Briatore. Ha letto della polemica sul turismo al sud, secondo lui poco sensibile ai bisogni dei ricchi?
Non saprei dire se è così. So che con Briatore studiavo al geometra. Lui fu bocciato al secondo anno, poi lasciò e fece una scuola privata per recuperare tutti gli anni in uno. Credo sia la dimostrazione che il detto popolare - "ultimi a scuola, primi nella vita" - è vero.
- Beppe Grillo: "È un minus habens". I grillini: "Peggio di lui". In generale: "Il novanta per cento delle persone è stupido. In un paese di 60 milioni di abitanti come l’Italia, saranno all’incirca 54 milioni: non possono essere andati tutti alla festa nazionale dei 5 stelle a Palermo".
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. -- Contro la paura dei numeri, una nuova rivista ("Mate. Da zero all’infinito") pubblicata dalla editrice Centauria.22 aprile 2016, di Federico La Sala
- ARITMETICA E ANTROPOLOGIA. UNA DOMANDA AI MATEMATICI: COME MAI "UN UOMO PIU’ UNA DONNA HA PRODOTTO, PER SECOLI, UN UOMO" (Franca Ongaro Basaglia)?! Non è il caso di ripensare i fondamenti?!
La sfida dei numeri è letterariadi Piergiorgio Odifreddi (la Repubblica, 17.04.2016)
La matematica, come si sa, è la Cenerentola della cultura: un po’ dovunque, ma soprattutto in Italia. È difficile immaginare che la sua storia si concluderà felicemente come nella fiaba, con qualche principe azzurro che la sposerà. Ma ogni tanto, almeno, sulla porta di casa la matematica può appendere un fiocco rosa, per annunciare un suo qualche parto: verginale, ovviamente.
È il caso della nuova rivista mensile Mate, che reca come sottotitolo Da zero all’infinito. È pubblicata dalla casa editrice Centauria, e il suo primo numero si troverà in tutte le edicole da questo mercoledì. Avrà 100 pagine e sarà disponibile sia in edizione cartacea che digitale, per tablet o cellulare. Il suo direttore, Luciano Regolo, ha dichiarato che la rivista vuole «cercare di sfatare il pregiudizio che la matematica sia appannaggio di pochi eletti». Una sfida che verrà affrontata «offrendo uno spaccato di quanto numeri e formule siano nella nostra quotidianità, nella natura, nell’arte e nel tempo libero, nel nostro passato, nel nostro presente e nel nostro futuro».
Ogni numero di Mate conterrà almeno un’intervista, oltre a dossier, studi, approfondimenti, spiegazioni di teoremi teorici e pratici, analisi dei legami con l’attualità, una ricca sezione di giochi e, dulcis in fundo, un “giallo del mese”: tutto a sfondo matematico, ovviamente. Auguri, dunque, e 1000 numeri!
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. Odifreddi dà alla matematica l’onore di grande motore della civiltà, ma ancora non sa «Che cos’è il numero, che l’uomo lo può capire? E che cos’è l’uomo, che può capire il numero?». La sua recensione di un saggio di Alex Bellos, con alcune note - di Federico La Sala11 febbraio 2016, di Federico La Sala
I contributi delle donne alla scienza: ieri e oggi
di Margherita Hack *
La storia delle donne nella cultura e nella vita civile è stata una storia di emarginazione fino alla fine dell’Ottocento e in gran parte ancora fino alla metà del Novecento, almeno nei paesi industrializzati. In molti paesi in via di sviluppo, salvo rare eccezioni, le donne sono ben lontane non solo dall’aver raggiunto la parità con l’altro sesso, ma anche dal vedere loro riconosciuti i più elementari diritti di esseri umani. Quali possono essere le cause di questa situazione che risale indietro nei secoli? Forse già nelle epoche preistoriche, la forza fisica necessaria per sopravvivere, le numerose gravidanze e il lungo periodo di allattamento e di cura della prole hanno portato alla differenziazione dei compiti. Oggi, i progressi della scienza e della medicina, e le conseguenti applicazioni tecnologiche hanno annullato la condanna biblica - uomo lavorerai con fatica, donna partorirai con dolore - almeno nei paesi industrializzati.
Per secoli le donne che potevano avere accesso all’istruzione erano quelle rinchiuse nei conventi. Forse per questo le donne che sono emerse nel passato erano soprattutto umaniste, pittrici, scrittrici, poetesse, ma molto più raramente scienziate. Infatti chi ha attitudini artistiche o letterarie può emergere anche senza una preparazione specifica, mentre le scienze, e in particolare le cosiddette scienze "dure" come matematica e fisica richiedono una preparazione di base, senza la quale è quasi impossibile progredire. Solo quelle poche favorite dall’avere un padre, un fratello o un marito scienziato disposto a condividere le proprie cognizioni, potevano farsi una cultura scientifica. Basta ricordare che ancora all’inizio del XX secolo in molti paesi europei alle ragazze era precluso l’accesso alle università ed anche ai licei.
Perciò le donne, escluse dalle università, escluse dall’educazione scientifica, sono emerse là dove potevano emergere. Così è sorto il pregiudizio secondo cui le donne sarebbero più adatte alle materie letterarie e linguistiche che non a quelle scientifiche. Le stesse ragazze crescono in mezzo a questi pregiudizi e se ne lasciano influenzare, e scelgono le facoltà umanistiche anche contro le loro naturali inclinazioni, contribuendo così a rafforzare i pregiudizi stessi. Comunque oggi cresce sempre di più il numero di ragazze che scelgono materie ritenute tipicamente maschili come ingegneria.
Malgrado le difficoltà incontrate, non sono poche le scienziate che hanno portato importanti contributi allo sviluppo della scienza. La storia ci tramanda i nomi di alcune famose scienziate. Ce ne furono una ventina nell’antichità, fra cui emerge il nome della matematica Ipazia; solo una decina nel medioevo, soprattutto nei conventi, quasi nessuna tra il 1400 e il 1500, 16 nel 1600, 24 nel 1700, 108 nel 1800. Oggi solo nel campo dell’astronomia sono più di 2000, ed in ogni campo dei sapere le ricercatrici universitarie superano il 50%, con punte ded’80% nelle facoltà umanistiche, del 60% in quelle di scienze biologiche, dal 30 al 40% nelle scienze abiologiche, più dei 50% nelle matematiche, mentre sono ancora al di sotto dei 20% in facoltà come ingegneria e agraria.
Fra le matematiche va ricordata la già citata Ipazia (370-415 d.C.), figlia del matematico e filosofo Teone. Diventò capo di una scuola platonica di Alessandria d’Egitto frequentata da molti giovani. Fu uccisa barbaramente da monaci, forse anche perché tanta genialità matematica in una donna poteva sembrare indice di empietà. Nel 1700 Maria Gaetana Agnesi (1718-1799) fu la prima donna ad essere chiamata a ricoprire una cattedra universitaria, all’Università di Bologna, e Sophie Germain (1 776-183 1) fu una riconosciuta esperta di teoria dei numeri e di fisica. Nel XIX secolo ci sono numerose grandi matematiche, fra le quali emergono soprattutto Sofia Kovaleskaja (1850-1891), professore all’Università di Stoccolma, e Emmy Noether (1882-1935), fondatrice dell’Algebra moderna. Fra le matematiche italiane di questo secolo ricordo Pia Nalli ( 1866-1964) professore ordinario di analisi matematica all’università di Cagliari e poi di Catania; Maria Pastori (1895-1975) ordinario di Meccanica Razionale all’università di Messina, Maria Cibrario Cinquini (1905-1992), ordinario di Analisi matematica a Cagliari e professore emerito dell’università di Pavia, Maria Biggiogero Masotti ordinario di geometria presso il Politecnico di Milano.
Fra le fisiche e le astrofisiche vanno ricordate, naturalmente Marie Sklodwska Curie (1867-1934), premio Nobel per la fisica nel 1903 e per la chimica nel 1911, e prima donna professore alla Sorbona e la figlia Irene Curie (1897-1956) premio Nobel per la chimica nel 1935; Lise Meitner (1878-1856) premio Nobel per la chimica nel 1935; Lise Meitner (1878-1968) che scopre il fenomeno della fissione nucleare ed è la prima donna ad avere una cattedra universitaria di fisica in Germania; Marie Goeppert Mayer (1906-1972) premio Nobel per la fisica nel 1963 per la sua teoria sui "numeri magici" che determinano la stabilità degli atomi; Wu Chieng-Shiung (1913-1997), professore di fisica alla Columbia University, scopritrice della non conservazione della parità nelle interazioni deboli.
Fra le astronome e astrofisiche va ricordata Caroline Herschel (1750-1848) che insieme al fratello William iniziò lo studio fisico del cielo, occupandosi di quello sfondo di stelle fino allora considerato poco più di uno scenario su cui si muovevano i pianeti. A loro si deve lo studio delle nubi interstellari, la scoperta di regioni apparentemente prive di stelle, che oggi sappiamo essere regioni ricche di polveri che ci nascondono le stelle retrostanti, e lo studio della distribuzione delle stelle sulla volta celeste.
Maria Mitchell (1818-1889) è stata la prima famosa astronoma americana, docente di astronomia al Vassar College e direttrice di quell’osservatorio, che ha preso il suo nome.
Un terzetto di astronome americane che hanno legato il loro nome a scoperte e ricerche fondamentali per la moderna astrofisica sono Henrietta Swan Leavitt (1868-1921), Anne Cannon (1863-1941) e Antonia Maury (1866-1952). La prima scoprì la relazione che lega il periodo di variazione di luce di una classe di stelle variabili dette "Cefeidi" al loro splendore assoluto, facendo di questa classe di stelle uno dei migliori mezzi per la determinazione delle distanze delle galassie. Alla seconda si deve la classificazione degli spettri di più di 225.000 stelle; il risultato del suo lavoro è raccolto nel poderoso catologo "Henry Draper" (dal nome dei finanziatone dell’opera) che è ancora oggi largamente consultato. La terza scoprì alcune caratteristiche degli spettri stellari, che permettevano di stabilire lo splendore assoluto di una stella, e quindi - misurato lo splendore apparente - risalire alla distanza. Essa ha anticipato di almeno due decenni il metodo di determinazione delle distanze dal semplice studio dello spettro.
Una grande astrofisica, iniziatrice dei metodi di studio delle atmosfere stellari e della determinazione della loro composizione chimica è stata Cecilia Payne Gaposchkin (1890-1979). Iniziatrice dello studio dell’evoluzione chimica della Galassia è stata una giovane astrofisica, Beatrice Tinsley, scomparsa prematuramente una ventina di anni fa. Oggi sono numerosissime le astrofisiche di fama internazionale che guidano gruppi di ricerca nei più svariati campi, dalla fisica stellare alla cosmologia, e delle più svariate nazionalità. Si può stimare che in tutto il mondo rappresentino dal 25 al 30% di tutti gli astronomi e astrofisici.
Altrettanto numerose sono le scienziate nel campo della biologia e delle scienze mediche, molte insignite di premio Nobel. Per tutte ricordiamo Rita Levi- Montalcini (1909) premio Nobel per la medicina nel 1986.
Sebbene oggi i contributi delle donne alla scienza vengano riconosciuti, resta il fatto che le scienziate per emergere devono generalmente lavorare di più dei loro colleghi e devono ancora superare numerosi pregiudizi, che, contrariamente a quanto si crede, sono maggiori nei paesi anglosassoni che non in quelli latini.
Spesso mi viene chiesto se ho incontrato molte difficoltà nel corso della mia vita scientifica. Ritengo che molti degli ostacoli di cui si lamentano parecchie ricercatrici dipende anche dall’educazione ricevuta che, almeno fino a qualche decennio fa, tendeva a fare delle bambine persone arrendevoli e servizievoli, poco combattive e desiderose di protezione. Oggi mi sembra che le cose vadano cambiando, la vita e l’educazione comune a bambini e bambine li lascia più liberi di sviluppare le proprie attitudini naturali, senza imporre loro condizionamenti dovuti al sesso.
lo ho avuto la fortuna di avere una famiglia in cui babbo e mamma erano perfettamente eguali, si dividevano i compiti in piena parità, e che non mi hanno mai imposto comportamenti o giocattoli legati a stereotipi sessuali. Anche lo sport che ho praticato per parecchi anni mi ha aiutato a sviluppare quella competitività che e necessaria per riuscire nell’atletica come nella scienza, per vincere sportivamente, allenandosi e studiando e avendo la costanza di perseguire lo scopo di battere un record o di ottenere un risultato scientifico, senza scoraggiarsi davanti agli insuccessi, perseverando con costanza. Credo perciò che l’ambiente familiare in cui ho avuto la fortuna di nascere sia stato estremamente importante per darmi fiducia nelle mie possibilità, e per non provare complessi di inferiorità che ho spesso notato in colleghe della mia generazione e anche più giovani.
Malgrado i grandi progressi fatti dalle donne, ci sono ancora notevoli disparità nel mondo del lavoro, della politica e della ricerca. Nelle università per esempio le ricercatrici sono ormai più della metà di tutti i ricercatori, ma appena si passa al livello superiore, quello dei professori associati, le.donne sono meno del 30% e al più alto livello dei professori ordinari sono appena il 10%. In politica è a tutti nota la scarsa rappresentanza femminile alla camera dei deputati e al senato. Al governo dei comuni sono ancora una minoranza le donne sindaco, mentre sono frequenti gli assessorati alla cultura assegnati a donne, il che mi fa malignamente pensare quanta poca importanza i politici tendono ancora a dare alla cultura, ritenuta un trascurabile centro di potere locale. Quasi sempre si attribuisce questa scarsa presenza femminile nei livelli più alti all’impegno familiare, alle cure dei marito e dei figli, e si chiede un maggiore impegno dello stato nel fornire asili nido, scuole materne, scuole a tempo pieno. Giustissimo! Però rarissimamente si afferma il diritto delle donne e il dovere degli uomini di dividersi al 50% le cure familiari, dalle più umili alle più importanti, anche se la legislazione familiare dà alle donne la possibilità di rivendicare questa reale parità. Sta alle giovani donne educare i propri compagni e ai giovani uomini di incitare le loro compagne ad affermarsi nella vita.
Comunque ritengo che il crescente numero di donne affermate nella scienza, nella politica, nello sport e in tutti i campi dell’attività umana fornisca quei modelli che finora mancavano alle bambine, e che possono dar loro fiducia e stimoli ad eguagliarle.
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. --- Due neuroni per uno zero. Cosa succede nel cervello quando percepiamo l’insieme vuoto (di G. Vallortigara)17 gennaio 2016, di Federico La Sala
Due neuroni per uno zero
Una nuova scoperta mostra cosa succede nel cervello quando percepiamo l’insieme vuoto: è visto sia come un numero tra gli altri numeri posti in una scala sia come uno scarto tra nulla ed esistenza di qualcosa
di Giorgio Vallortigara (Il Sole-24 Ore, Domenica, 17.01.2016)
- Okuyama, S. et al. Representation of the numerosity «zero» in the parietal cortex of the monkey , Scientific Reports, 5, 10059; doi: 10.1038/srep10059
Provate a chiedere a un bambino di quattro, cinque anni, quando già sa recitare impeccabilmente la sequenza dei numeri naturali, «zero, uno, due, tre...», quale sia il numero più piccolo: molto probabilmente vi risponderà che è l’uno e non lo zero. C’è una fase dello sviluppo cognitivo in cui l’uso del simbolo «zero» per indicare l’assenza di qualcosa non è ancora accompagnato da una piena comprensione delle relazioni d’ordine tra lo zero e gli altri numeri. Lo sviluppo storico del pensiero matematico sembra ricapitolare queste difficoltà. L’introduzione di una notazione simbolica per lo zero è relativamente recente. L’impiego dello zero come un vero numero, manipolabile aritmeticamente, compare, in India, tra il terzo e il sesto secolo (i Babilonesi usavano lo zero solo con funzione di segnaposto, e lo stesso pare abbiano fatto i Maya e gli antichi Cinesi).
In questi ultimi anni, però, abbiamo imparato che creature del tutto prive di un simbolo per lo zero, come gli animali delle altre specie o i bambini più piccoli, possono nondimeno cogliere l’idea di un insieme vuoto e rappresentarselo come un’autentica entità numerica. Per farlo impiegano quello che gli scienziati definiscono «sistema approssimato del numero» o, in termini più colloquiali, «senso del numero».
Il segno distintivo del senso del numero è l’«effetto distanza». Si fa prima e si commettono meno errori a decidere, per esempio, se sia più grande «otto» o «diciotto», che non «otto» e «dodici». La prestazione è cioè tanto migliore quanto più i due numeri sono distanti. Lo stesso accade se anziché usare simboli come i numeri arabi si mostrano sullo schermo di un computer degli insiemi di pallini di differenti numerosità. E’ notevole che nei due casi succeda la stessa cosa.
Con i simboli, infatti, molti aspetti diversi potrebbero causare confusione: ad esempio, il fatto che i simboli si assomiglino fisicamente («otto» e «diciotto» hanno l’«otto» in comune, che invece «otto» e «dodici» non hanno) oppure che si assomiglino i suoni che produciamo per pronunciarli (i suoni per «otto» e «diciotto» si somigliano di più dei suoni per «otto» e «dodici»). Eppure tutto ciò non importa: è come se, per eseguire il confronto, i suoni o i segni dei simboli fossero convertiti automaticamente nel cervello nei valori delle rispettive quantità.
Il senso del numero è ubiquo nel mondo animale, si ritrova nei pesci e negli uccelli, nei mammiferi e negli anfibi, forse perfino negli insetti come le api, e supporta una matematica approssimata che consente di effettuare le operazioni aritmetiche (somme, sottrazioni, divisioni).
Adesso immaginate un semplice esperimento nel quale si debbano ordinare delle quantità non simboliche, come appunto dei pallini sullo schermo di un computer. Compaiono sullo schermo, poniamo, un insieme di otto pallini e uno di dodici pallini; poi uno di otto e uno di diciotto... e così via. Ogni volta la consegna è di ordinare le due quantità, pigiando su un touch screen prima il numero più piccolo e poi quello più grande. è un compito che può imparare facilmente un bambino di età prescolare, ma anche una scimmia.
Che accade se, quando l’apprendimento è ormai ben consolidato, sullo schermo vengono presentate delle coppie nelle quali uno dei due insiemi di pallini è pari a «zero» (cioè costituito di nessun pallino)? I bambini, ma anche le scimmie, rispondono correttamente: prima pigiano in corrispondenza dell’insieme vuoto e poi del numero (lo fanno anche quei bambini che quando sono interrogati verbalmente su quale sia il numero più piccolo nella serie dei numeri rispondono che è l’uno anziché lo zero). E siamo certi che questa dell’insieme vuoto sia davvero una rappresentazione numerica, perché anche qui fa la sua apparizione la firma caratteristica del senso del numero: l’effetto distanza. Si fa prima a dire che zero pallini è più piccolo di dodici pallini che non a dire che zero pallini è più piccolo di quattro pallini (e non c’entra quanta area occupano i pallini, perché l’effetto della distanza si osserva anche quando quattro pallini grandi occupano un’area maggiore di quella occupata da dodici pallini piccoli). Ma a cosa corrisponde, nel cervello, questa rappresentazione primitiva dell’insieme vuoto, dello zero pre-simbolico?
Già si sapeva che in una porzione posteriore del lobo parietale nella scimmia (e, con ogni probabilità, anche nella specie umana) ci sono neuroni la cui frequenza di scarica è modulata dalla numerosità. Ad esempio, ci sono neuroni che hanno un picco massimo di risposta quando l’animale vede cinque pallini o cinque quadratini o sente cinque suoni... insomma quando percepisce la «cinquità» di un insieme di elementi. La codifica della numerosità è continua e non discreta, così come ci si aspetta dal senso del numero: il neurone che risponde a «cinque» in maniera ottimale risponde un po’ meno al «sei» e al «quattro», ancor meno al «sette» e al «tre» e così via.
Ora però Okuyama e colleghi dell’Università Tohoku, in Giappone, hanno osservato che vi sarebbero due diversi tipi di neuroni per lo zero, neuroni a risposta «continua» che, come per le altre numerosità, hanno un massimo di frequenza di scarica per l’insieme vuoto (nessun pallino) e frequenze via via digradanti per le altre numerosità (un po’ di risposta a un pallino, un po’ meno a due pallini... e così via) e neuroni a risposta «esclusiva» che invece aumentano la frequenza di scarica solo quando c’è lo zero (l’assenza di pallini) e non presentano alcuna variazione di risposta per qualsiasi altra numerosità (un pallino, due pallini...).
Lo zero sta per il nulla, l’assenza anziché la presenza e, forse, possiede per questa ragione una rappresentazione neurale un poco speciale. Se poi il nulla sia qualcosa o non lo sia è un problema sul quale molto si sono affaticati i logici e filosofi medievali, e che non considereremo qui. Invece vale la pena notare che tra nulla e qualcosa, tra esistenza e non esistenza, potrebbe sussistere un’asimmetria cognitiva.
Alcuni esperimenti della psicologa cognitiva Karen Wynn hanno mostrato che infanti di otto mesi che vedono un oggetto occultato da uno schermo si meravigliano assai quando all’abbassarsi dello schermo l’oggetto appare essere scomparso. Gli infanti, cioè, ritengono che anche se non lo vedono più, l’oggetto continui ad esistere dietro lo schermo. Tuttavia quel che vale per l’assenza non sembra esser vero per la presenza. Se vedono che un oggetto è stato sottratto da dietro uno schermo che l’occultava, non si meravigliano poi di vederlo «magicamente» ricomparire quando lo schermo viene abbassato. Difficile asserire se per loro sia un nuovo oggetto, un sosia, o lo stesso oggetto.
Su Tlön, il pianeta immaginato da Borges in Tlön, Uqbar, Orbis Tertius (http://24o.it/pPjzyY), le cui nazioni «sono - in maniera congenita - idealiste» non è infrequente la duplicazione degli oggetti perduti: «Due persone cercano una matita, la prima la trova e non dice nulla; la seconda trova una seconda matita, non meno reale, ma più conforme alle sue aspettative». Sul nostro pianeta, invece, fino a una certa età, la rappresentazione della presenza di un oggetto sembra slegata da quella della sua assenza: gli oggetti non possono magicamente scomparire, ma possono magicamente apparire. Forse i neuroni che segnalano lo zero come entità continua si sviluppano prima o in modo distinto da quelli che segnalano l’assenza in modo discreto. Così quando vi sono elementi da contare i bambini intuiscono che zero è un numero: il valore minimo nel continuo rappresentato dal sistema analogico del senso del numero. Ma se non c’è una quantità contabile, allora resta solo la rappresentazione del subitaneo assurgere all’esistenza di un «qualcosa» o, forse, tramite i neuroni a risposta discreta, di quel qualcosa la vertiginosa assenza.
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. --- "MECCANICISMO" (G. ISRAEL). L’esperienza umana non è riducibile ad algoritmi (di Michele Emmer)6 dicembre 2015, di Federico La Sala
Saperi. L’esperienza umana non è riducibile ad algoritmi: l’attacco di Giorgio Israel agli eccessi del meccanicismoL’abuso della matematica
I modelli che funzionano bene nel campo della fisica mostrano gravi limiti se applicati alle scienze sociali
Non possono dirci che cosa succederò nell’economia
di Michele Emmer (Corriere della Sera, La Lettura, 06.12.2015)
- GIORGIO ISRAEL, Meccanicismo. Trionfi e miserie della visione meccanica del mondo, Zanichelli, Pagine 322, e. 28.
Olivier Peyon ha realizzato nel 2013 un documentario dal titolo Comment j’ai détesté les maths. In realtà il film vuole essere un elogio dei matematici, della loro vita di ricercatori, della loro passione. Alla fine del film intervengono due matematici che si sono occupati di economia, George Papanicolaou, greco, e Jim Simons, che, dopo una brillante carriera scientifica, è diventato un ricco uomo d’affari creando il fondo speculativo Renaissance Technologies.
Parla della matematica economica e dei dannati algoritmi che hanno mandato in rovina l’economia globale, rendendo lui miliardario con le speculazioni sulla finanza virtuale. Per Papanicolaou gli algoritmi matematici di Simons non erano stati testati a sufficienza. Nessuno sapeva in che modo avrebbero reagito in situazioni di emergenza. Insomma, ci si può fidare della matematica?
Di matematica, matematica applicata e modelli matematici parla il libro di Giorgio Israel Meccanicismo (Zanichelli), pubblicato poco dopo la morte dell’autore. Nel film di Peyon, Cedric Villani, direttore dell’Institut Poincaré di Parigi, afferma che la separazione tra matematica e matematica applicata è superata. Frasi tipo quelle di G. H. Hardy, scritte nel 1940 per elogiare la matematica inutile, oggi non hanno senso. Hardy non sapeva che a Bletchley Park, matematici, fisici, ingegneri stavano lavorando alla decriptazione del codice nazista Enigma, usato in guerra per rendere incomprensibili i messaggi. Tra quei matematici Alan Turing, alla cui vita è dedicato il film Imitation Game, Oscar per la miglior sceneggiatura non originale.
Uno dei problemi centrali del libro di Israel è la questione della applicabilità di modelli e metodi matematici nelle discipline non strettamente matematiche e fisiche, in particolare all’economia e alle scienze sociali. Il capitolo «Oltre il mondo inanimato» si apre con una frase del matematico dell’Ottocento Augustin Cauchy: «Coltiviamo con ardore le scienze matematiche, senza volerle ostentare al di là del loro dominio; non illudiamoci che si possa affrontare la storia con delle formule, né sanzionare la morale con dei teoremi o del calcolo integrale». Israel parte da Galileo, dall’«idea che la struttura su cui Dio ha edificato il mondo è la matematica». Ma in nessun modo si può pensare che Galileo «includesse nel “mondo” anche la sfera dell’uomo, della soggettività, del pensiero».
Poi abbiamo i tentativi di trovare un equo sistema elettorale del matematico Condorcet, alla vigilia della Rivoluzione francese, e i modelli per lo studio della diffusione del vaiolo alla metà del Settecento da parte di Daniel Bernoulli, con l’introduzione del calcolo delle probabilità. Il primo modello matematico per l’economia è di Dupont de Nemours alla fine del Settecento: «L’aspetto più interessante da evidenziare - scrive Israel - è l’importanza attribuita alla nozione di equilibrio, che testimonia l’influsso della mentalità fisico-matematica, del modello della meccanica, e di un indirizzo che la matematizzazione dell’economia, e più in generale delle scienze sociali, sta prendendo».
Agli inizi del Novecento la svolta, con i modelli per la dinamica delle popolazioni, l’epidemiologia matematica. Ed ecco la motivazione di Israel: «Conosciamo bene la versione più famosa e influente del riduzionismo, la concezione epistemologica che tende a formulare i concetti e il linguaggio di una teoria scientifica nei termini di una teoria considerata fondamentale. È l’argomento centrale di questo libro: il meccanicismo, che consiste nel ritenere che tutti i fenomeni si riducono a fenomeni di moto, per cui il fine fondamentale della scienza è ricondurre ogni forma di conoscenza alla meccanica». Ed è questa la malattia di fondo delle teorie matematiche utilizzate in ambiti non matematici e fisici.
Il matematico von Neumann nel 1932 scrive: «Le scienze non cercano di spiegare, a malapena tentano di interpretare, ma fanno soprattutto modelli. Per modello si intende un costrutto matematico che, con l’aggiunta di interpretazioni verbali, descrive dei fenomeni osservati. La giustificazione è soltanto e precisamente che funzioni, descriva correttamente i fenomeni in un’area abbastanza ampia, e soddisfi dei criteri estetici, cioè deve essere piuttosto semplice». Nei modelli biologici, a partire dalla dinamica delle popolazioni, via via che la complessità del sistema aumenta, non si ha un aumento di stabilità bensì del suo contrario.
Si trattava quindi di mettere in discussione i modelli matematici, cosa che, sottolinea Israel, non è mai stata lontanamente considerata. Tanto che nel 1976 i matematici Oster e Guckenheimer osservano: «Vi sono persone che affermano che non esiste un solo progresso nel campo della biologia che possa essere attribuito alle teorie matematiche. Quando entrano in gioco i sistemi complessi, il linguaggio appropriato è l’inglese, non quello matematico».
Alla luce delle ricerche recenti, ricorda Israel, «l’espansione della modellistica matematica in ambito biologico è diventata talmente frammentata da distruggere persino la possibilità di un confronto e sintesi tra le miriadi di modelli... malgrado alcune marginali differenze, si dimostra il ruolo centrale dell’analogia meccanica nel processo di fondazione dei più importanti settori della biologia matematica».
I successi predittivi della matematica in fisica non garantiscono analoghi successi in ambiti di natura ben diversa. Il tutto si complica ulteriormente quando si passa ai rapporti sociali ed economici. Entrano in gioco modelli teorici di matrice fortemente ideologica, come nel caso della teoria dell’equilibrio economico generale, i cui paradigmi fondazionali sono: dimostrare che l’equilibrio economico esiste, che tale equilibrio è unico, che il mercato possiede la virtù salvifica di realizzare tale equilibrio, purché non si introducano vincoli e legacci e l’azione dei singoli soggetti economici possa esplicarsi in piena libertà. Un paragrafo è dedicato alla scienza della complessità. «Il concetto di complessità - osserva Israel - continua a vagare in un limbo situato tra ontologia ed epistemologia. L’aspirazione a definirlo come una proprietà del mondo reale si scontra con la vaghezza delle definizioni di carattere empirico... D’altra parte ogni sua caduta nella sfera puramente epistemologica fa di esso una versione disillusa e pessimista del concetto di complicazione».
Le conclusioni di Israel: «La modellizzazione nell’ambito dei contesti non fisici non ha mai raggiunto neanche lontanamente l’ombra della precisione che ha raggiunto in gran parte dei contesti fisici... confrontare il grado di precisione che è possibile ottenere nel contesto dei fenomeni meccanici propriamente detti con quello sociale è desolante; nessun modello matematico è in grado di dire, neppure con un grado di approssimazione generoso, che cosa accadrà domani all’economia».
Un esempio è la valutazione della attività scientifica dei ricercatori mediante indicatori «oggettivi», che tendono a sostituire l’esame della qualità dei risultati. L’International Mathemathical Union ha osservato che si sta creando una cultura dei numeri per cui le istituzioni e gli individui credono che si possano ottenere decisioni eque mediante valutazioni algoritmiche e alcuni dati statistici. Non è certamente un caso che tale mitologia faccia presa su coloro che meno capiscono di numeri e scienza. Nell’ultimo capitolo si parla delle due culture, dello stretto legame tra letteratura, narrazione e matematica. Classico esempio la questione dell’infinito.
Nell’ Eloge des Mathématiques (2015) il filosofo francese Alain Badiou, invitando i filosofi a studiare la matematica moderna, scrive: «La matematica è la più convincente delle invenzioni umane per esercitarsi a quello che è la chiave sia di tutto il progresso collettivo comune che della felicità individuale: dimenticare i nostri limiti per arrivare all’universalità del vero». Dobbiamo ancora inventare e creare tanta matematica per affrontare le grandi questioni del nostro mondo, non solo nel senso di Galileo. Fortunatamente.
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. --- «Dovremmo essere tutti femministi», invita la Adichie. Perché l’unico numero primo pari è il due (di Melania Mazzucco)10 maggio 2015, di Federico La Sala
- MICHELANGELO E LA SISTINA (1512-2012). I PROFETI INSIEME ALLE SIBILLE PER LA CHIESA UN GROSSO PROBLEMA ....
 DOPO 500 ANNI, PER IL CARDINALE RAVASI LA PRESENZA DELLE SIBILLE NELLA SISTINA E’ ANCORA L’ELEMENTO PIU’ CURIOSO. Materiali sul tema, per approfondimenti
DOPO 500 ANNI, PER IL CARDINALE RAVASI LA PRESENZA DELLE SIBILLE NELLA SISTINA E’ ANCORA L’ELEMENTO PIU’ CURIOSO. Materiali sul tema, per approfondimenti
- DAL "CHE COSA" AL "CHI": NUOVA ERMENEUTICA E NUOVO PRINCIPIO DI "CARITÀ" (...)
 DELLA TERRA, IL BRILLANTE COLORE. Il libro di Federico La Sala offre un punto di vista raro. Quello di un pensiero maschile che osserva e riflette e su alcuni pilastri del pensero filosofico occidentale in modo non neutro (...) (E. Cirant)
DELLA TERRA, IL BRILLANTE COLORE. Il libro di Federico La Sala offre un punto di vista raro. Quello di un pensiero maschile che osserva e riflette e su alcuni pilastri del pensero filosofico occidentale in modo non neutro (...) (E. Cirant)
Siamo tutti femministi
Ridotta a macchietta, caricatura o anacronismo. Oppure recuperata con operazioni più glamour che politiche. Invece ora la più giusta rivoluzione del XX secolo ritorna
A patto di farla insieme agli uomini
Perché l’unico numero primo pari è il due
di Melania Mazzucco (la Repubblica, 10.05.2015)
DOVE eravamo rimasti col femminismo? In Occidente da almeno vent’anni la parola è andata fuori corso, come una vecchia moneta. Rottamata, liquidata, trasformata in un ironico insulto. Non fare la femminista. Non sarai mica femminista? Oppure in un anacronismo. Negli ultimi vent’anni per una donna proclamarsi femminista era un boomerang, come presentarsi a un party con un vestito fuori moda. Una dichiarazione di inattualità, un modo sicuro per raccogliere l’esecrazione universale - anche di molte fra quante, a loro tempo, furono orgogliose di esserlo. Il rancido dibattito sugli errori e sui fallimenti del femminismo storico è diventato un pretesto per affossare, con la parodia del femminismo, e delle femministe, l’unica giusta rivoluzione del Ventesimo secolo.
Ci voleva una bravissima scrittrice nigeriana, Chimamanda Ngozi Adichie, che sa essere diretta senza essere semplice, sia quando inventa romanzi sia quando recita una conferenza di trenta minuti, per riaccendere l’attenzione. Poi una star planetaria come Beyoncé ha campionato alcune frasi del discorso di Adichie, Dovremmo essere tutti femministi, inserendole nella sua canzone Flawless, e la parola “femminista” è diventata di nuovo attraente. Fotografie patinate con la parola femminista in bella vista dietro l’icona di una giovane donna di successo, vibranti discorsi di attrici intelligenti e graziose davanti a platee attonite di signori attempati hanno completato il recupero del concetto - rendendolo glamour per le nuove generazioni: l’operazione di marketing, o di restyling, è perfettamente riuscita. Ma forse non si tratta solo di questo. Liberato dalla zavorra dell’ideologia, ricondotto ai comportamenti minimi della vita quotidiana, questo neofemminismo “pop”, o “light” (copyright Annie Lennox), ha avuto il grande merito di ricominciare a far discutere di disuguaglianza. Perché è di questo che si tratta.
Letteralmente, femminista è «persona che crede nell’eguaglianza sociale, politica, giuridica ed economica dei sessi». Potrebbe sembrare una convinzione ormai acquisita, trascorso più di un secolo dalle prime rivendicazioni delle suffragette (che chiedevano, si badi, il diritto di voto alle elezioni, cioè semplicemente la voce, ovvero la fine di una millenaria esclusione e segregazione): oggi non si incontra nessuno che pubblicamente osi proclamarsi in disaccordo, e osi riesumare i vecchi stereotipi dell’inferiorità mentale, o biologica, della donna.
Ma - al di là delle buone intenzioni e della correttezza politica di facciata - questa parità che tutti teoricamente ritengono cosa buona e giusta, nella società, nella politica, nel diritto, nell’economia, è stata raggiunta? Per rispondere, bisogna tener conto di troppe differenze - geografiche, culturali, economiche, anagrafiche, religiose - e forse questa è già la risposta.
Non è stata raggiunta la parità se, facendo lo stesso mestiere e avendo le stesse qualifiche, gli stessi diplomi, la stessa esperienza, una donna guadagna meno di un uomo, solo perché è una donna. Se a casa, a scuola, all’università, in azienda, non ha realmente le stesse opportunità dei suoi compagni. Se il lavoro per lei è un miraggio o un lusso, se lo studio è un privilegio, se la famiglia è un’alternativa o una missione, se l’indipendenza è una colpa, se ritrovare la libertà dopo un rapporto o un matrimonio sbagliato è un crimine da pagare con la vita. Se anche solo dover dimostrare di valere qualcosa pretende il sacrificio della sua identità (meglio non sembrare troppo donna, se vuoi essere presa sul serio).
La parità non è equivalenza. Essere uguali non è essere identici. Su questo equivoco si è giocato il destino del femminismo storico - che i suoi avversari hanno facilmente ridotto a fenomeno psicosessuale, stigmatizzando la femminista come una virago ambiziosa e rabbiosa, una donna frustrata e negata che vuole prendere il posto dell’uomo diventando come lui, assumendone modi e comportamenti, ed esercitando il potere allo stesso modo.
Da qui anche la caricatura che, in questi anni di riflusso, si è a poco a poco stratificata nell’immaginario collettivo del Ventunesimo secolo: nella versione apocalittica la femminista essendo sinonimo di donna sgradevole e poco attraente, refrattaria alla depilazione, che siccome non piace agli uomini li detesta; nella versione integrata di manager single, anaffettiva, sterile e crudele tagliatrice di teste (nuova incarnazione dell’eviratrice che ossessionò il pensiero misogino di fine Ottocento). Invece la parità è altro. Si può essere pari essendo differenti. Per essere pari, inoltre, bisogna potersi dividere per due. Eccetto il due, i numeri primi sono tutti dispari. Non si può essere femministe da sole.
Fino a oggi, stranamente, si è sempre declinato il sostantivo al femminile - sia al singolare sia al plurale. La femminista, le femministe. Come se fosse un problema che riguardava solo le donne, e il loro modo di stare al mondo. Invece, è necessaria una piccola, ma immensa, rivoluzione grammaticale. «Dovremmo essere tutti femministi», invita la Adichie. Perché anche gli uomini, di oggi ma soprattutto di domani, possono esserlo (e in verità, parecchi già lo sono: basti pensare ai mutamenti che hanno ri-orientato i traguardi dell’esistenza, liberato le manifestazioni degli affetti e delle emozioni, capovolto la dinamica della genitorialità e parentalità, perfino i canoni dell’estetica). In fisica, la parità è una proprietà di simmetria della funzione: invertendo il segno alle coordinate spaziali un fenomeno si ripete immutato. Se questo nuovo femminismo basico avrà un futuro sarà proprio perché cerca di spostarci insieme. Di cambiare il segno alle coordinate dello spazio, del tempo, dell’educazione che diamo o vogliamo dare ai bambini, delle relazioni fra i generi, e - anche o soprattutto - con noi stesse. Esistono anche femministi felici.
* L’ANTICIPAZIONE Dovremmo essere tutti femministi di Chimamanda Ngozi Adichie (Einaudi, traduzione di Francesca Spinelli, pagg. 50, euro 9)
- MICHELANGELO E LA SISTINA (1512-2012). I PROFETI INSIEME ALLE SIBILLE PER LA CHIESA UN GROSSO PROBLEMA ....
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. ---- ALLA RICERCA DELLA VERA NATURA DELLA MATEMATICA. Gabriele Lolli propone un affascinante viaggio fra problemi e teoremi, affrontati come fiabe o miti (di Federico Peiretti -La matematica è poesia grazie a Calvino). ).28 febbraio 2011, di Federico La Sala
Scienza e fantasia. Una logica rilettura delle «Lezioni americane»
 La matematica è poesia grazie a Calvino
La matematica è poesia grazie a Calvino"Leggerezza, rapidità, esattezza, visibilità, molteplicità e coerenza: sei parole per definire il mondo dei numeri. Gabriele Lolli propone un affascinante viaggio fra problemi e teoremi, affrontati come fiabe o miti"
di Federico Peiretti (La Stampa/Tuttolibri, 05.01.2011)
Nell’estate del 1985 Calvino stava preparando una serie di lezioni che avrebbe dovuto tenere all’Università di Harvard. Sei lezioni per mettere in evidenza «alcuni valori della letteratura - scriveva Calvino - che mi stanno particolarmente a cuore, cercando di situarle nella prospettiva del nuovo millennio». Scelse per questo sei parole, ognuna delle quali, secondo lui, evidenziava un carattere essenziale della letteratura: leggerezza, rapidità, esattezza, visibilità, molteplicità e coerenza. Stava terminando il suo lavoro, quando improvvisamente morì, il 19 settembre 1985, all’età di 62 anni, e la sesta parola rimase incompiuta.
Le sue Lezioni americane sono la testimonianza di uno dei più grandi scrittori del Novecento sull’essenza del lavoro dello scrittore. Calvino vuole dimostrare che matematica e poesia hanno praticamente la stessa struttura. «L’atteggiamento scientifico e quello poetico coincidono - scrive - entrambi sono atteggiamenti insieme di ricerca e di progettazione, di scoperta e di invenzione».
Gabriele Lolli, docente di Filosofia matematica alla Normale di Pisa, logico eccellente, nel suo nuovo libro, Discorso sulla matematica , parte dalle Lezioni di Calvino per proporre un percorso inverso: dalla letteratura alla matematica. Questo per dimostrare che l’analisi di Calvino, sui fondamenti della letteratura, ben si adatta all’analisi del pensiero matematico. «Le Lezioni sono un racconto filosofico sulla matematica - osserva Lolli - un racconto che, grazie alla raffinatezza di Calvino, trasmette alla matematica tutta la bellezza e il fascino della letteratura».
E Lolli parte proprio dalle sei parole scelte da Calvino: «Vogliamo parlare della matematica - afferma - usando le stesse parole che Calvino ha rivolto alla letteratura». E questo per convincere il lettore che la matematica è poesia. Un lettore non prevenuto naturalmente, che non abbia avuto con la matematica soltanto un rapporto scolastico conflittuale. A facilitare il compito di Lolli c’è sicuramente l’interesse per la scienza e in particolare proprio per la matematica di Calvino, la sua amicizia con Primo Levi e la sua adesione, negli Anni Sessanta, quando si trasferì a Parigi, al gruppo dell’Oulipo, fondato da alcuni scrittori e matematici francesi, che perseguivano l’obiettivo di una scrittura che fosse «immaginazione scientifica, linguaggio logico e struttura matematica». E’ originale e seducente il lavoro di Lolli: «Convivono nella matematica - scrive - il fascino dell’esattezza scientifica e dell’infinita indeterminatezza del mondo dell’anima». Un bel teorema, Lolli ne è convinto, ha lo stesso valore e la stessa attrazione di una pagina di un grande scrittore, con una parte indefinita, aperta verso nuovi mondi, verso nuove dimostrazioni, solo intuite.
Per seguire le sue riflessioni sono sufficienti le conoscenze di uno studente delle superiori. Ma il modo migliore per affrontare la lettura del libro è quello di mettere da parte i nostri ricordi scolastici, per scoprire le meraviglie del mondo matematico lungo i percorsi suggeriti da Lolli. Si prenda, ad esempio, uno dei teoremi che ci propone di analizzare, molto semplice, la dimostrazione dell’uguaglianza degli angoli alla base di un triangolo isoscele. Dimentichiamo la dimostrazione meccanica che si trova sulla maggior parte dei testi scolastici e seguiamo il suo consiglio di «lasciar vagare la fantasia», inventando noi una nostra personale dimostrazione. Forse meno bella di quella di Euclide, ma solo così scopriremo che il procedere del ragionamento scientifico segue le stesse regole del racconto e della poesia: «Nessuno ha il coraggio di dire agli studenti che la matematica è come le fiabe - scrive Lolli - perché non sembrerebbe serio, ma se si vuole entrare nel mondo della matematica bisogna essere consapevoli che ci si deve atteggiare come nei confronti delle fiabe, o dei miti».
Il libro di Lolli presenta una serie straordinaria di spunti e riflessioni, alla ricerca della vera natura della matematica. Alla fine il matematico dovrebbe essere portato a chiedersi che cosa stia facendo, di che cosa si occupi e lo stesso dovrebbe fare l’insegnante di matematica, cercando di capire che cosa stia insegnando e anche lo studente dovrebbe chiedersi che cosa stia studiando. Solo se riusciremo a liberare la nostra fantasia scopriremo che un teorema di Pitagora o di Euclide, di Hilbert o di Gödel sono belli quanto una poesia di Leopardi o un racconto di Calvino. E per questo sarebbe necessario partire dalla scuola, con una rivoluzione didattica copernicana, che metta al centro lo studente e non un programma di formule e calcoletti, sovente inutili. Ma qual è la scuola disposta a liberare la fantasia?
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. ---- LA MATEMATICA DEL FUTURO. mostra: MATEMATICA SENZA NUMERI è dedicata ai bambini dai 3 ai 12 anni, e si svolge ad Explora, il Museo dei Bambini di Roma (di Roberto Natalini).28 febbraio 2011, di Federico La Sala
LA MATEMATICA DEL FUTURO
di Roberto Natalini *
È stata inaugurata ieri, 25 febbraio, a Roma, presso Explora, il museo dei bambini di Roma, la mostra Matematica senza numeri”(*). Avendo partecipato come consulente scientifico all’elaborazione di questo evento, affiancato in questo compito dalle bravissime Cristiana Di Russo e Alice Sepe, rischio di essere parziale nel raccontarvi di cosa si tratta, per cui fate un’ampia tara su quanto segue.
Intanto cosa vuol dire fare una mostra di matematica? E per bambini dai 3 ai 12 anni per giunta? Beh, è proprio quello che ci siamo chiesti noi, quando lo staff di Explora, condotto da Patrizia Tomasich, ci ha proposto di organizzare qualcosa di questo genere insieme. La matematica è sempre un po’ difficile da raccontare. Ci sono le formule, i numeri, e quelle cose dai nomi complicati che non si ricordano mai. E c’è l’ansia con cui molti l’affrontano. Se volete fare una mostra in cui i bambini possano giocare anche senza animatori, non vi siano nei paraggi touchscreen o altre diavolerie elettroniche, e soprattutto volete che i bambini si divertano, ma si divertano davvero, allora l’impresa è tutt’altro che facile. E se vogliamo includere bambini in età pre-scolare, allora diventa davvero disperata.
Eppure a me sembra che i bambini siano meno impauriti degli adulti dalla matematica, spesso la trovano solo un po’ noiosa, quando associata ad attività ripetitive, come imparare le tabelline e simili. Allora abbiamo deciso di provare a fare cose che non si fanno a scuola. E per prima cosa abbiamo tolto i numeri. Non perché si debbano demonizzare, ma per provare a far vedere che esiste un’altra matematica, che anzi costituisce la maggior parte di quello che i matematici studiano veramente (vi sfido a trovare tanti numeri in un articolo di matematica moderno. Lettere greche quante ne volete, x e y come se piovessero, ma i numeri?). Bisogna allora tornare ai problemi e alle operazioni che si possono compiere per risolverli. Perché la matematica, come dice Enrico Giusti nel suo bel libro “Ipotesi sulla natura degli oggetti matematici”, nasce sempre da procedimenti pratici che utilizziamo per risolvere certi problemi (a volte interni alla matematica stessa). Per misurare un’area gli agrimensori egizi piantavano un paletto per terra e con una una fune tracciavano delle linee rette o dei cerchi e questa pratica, nel tempo, si è trasformata nei nostri oggetti geometrici elementari. Tutto nasce dai problemi, e dai gesti che facciamo per risolverli. E se ce lo scordiamo, perdiamo la possibilità di capire profondamente che cosa sia o meno matematicamente interessante.
E così abbiamo pensato di far giocare i bambini a fare gli architetti con le tassellazioni del piano e della sfera, scoprendo che un pallone da calcio non si può ricoprire usando solo esagoni, ma servono anche i pentagoni (e senza dimenticare le magiche tassellazioni di Penrose). Abbiamo pensato che giocando con gli specchi (e ce ne sono tanti) avrebbero potuto vedere meglio come si sfruttano le simmetrie. Che si sarebbero divertiti con rompicapi topologici e problemi con i grafi, per verificare la regola di Eulero sui nodi, passeggiando su una riproduzione in scala della città di Königsberg. O a rimontare un puzzle delle regioni d’Italia in cui nessuna regione confini con una dello stesso colore e usando solo quattro colori (ma basteranno?). O a giocare con un grosso rompicapo tridimensionale che si ottiene unendo dei policubi morbidi (si chiama cubo di soma e si trova in cubetti di 10 cm. di lato, i nostri hanno lati di 1 metro!). E altro ancora.
Questa idee all’inizio erano disegnini su pezzetti di carta, erano chiacchiere tra noi e il gruppo del museo Explora, erano cose-che-ci-sembrano-divertenti. Poi, in modo abbastanza misterioso per me, sono diventati oggetti tridimensionali, di legno, vetro, spago, e altri materiali a cui non saprei dare un nome. E dopo ancora sono diventate uno spazio in cui i bambini ridono e si divertono e capiscono molto più velocemente di quanto avrei mai immaginato.Che aspettate allora ad andarla a vedere questa mostra? Basta che vi procuriate un bambino (e se siete un bambino, allora vi serve un adulto che vi accompagni...).
(*) MATEMATICA SENZA NUMERI è dedicata ai bambini dai 3 ai 12 anni, e si svolge ad Explora, il Museo dei Bambini di Roma http://www.mdbr.it/, dal 25 febbraio al 31 dicembre 2011. Il progetto è stato realizzato grazie al Bando ex art. 4 Legge 6/2000 del MIUR, Ministero dell’Istruzione, dell’Università e della Ricerca, ed in collaborazione con l’Istituto per le Applicazioni del Calcolo “M.Picone” - Consiglio Nazionale delle Ricerche, per i contenuti scientifici. È stata realizzata inoltre grazie al contributo di Finmeccanica e della Fondazione IBM Italia.
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. --- UNA NOTA SUL "DISAGIO DELLA CIVILTA’". Se le donne non "contano", non sanno nemmeno contare; e gli uomini, se "contano", altrettanto non sanno nemmeno contare!!!23 febbraio 2011, di Federico La Sala
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. --- La via per ricostruire una società decente. Ecco come si fa la rivoluzione culturale (di Serge Latouche).25 febbraio 2011, di Federico La Sala
Ecco come si fa la rivoluzione culturale
di Serge Latouche (l’Unità, 25 febbraio 2011)
La via della decrescita è un’apertura, un invito a trovare un altro mondo possibile. Questo altro mondo noi lo chiamiamo società della decrescita. L’invito è a viverci, qui e ora, e non in un ipotetico futuro che, per quanto desiderabile, forse non vedremo mai. Questo altro mondo dunque sta anche in quello in cui viviamo oggi. Sta anche in noi. La via è anche uno sguardo, un altro sguardo sul nostro mondo, un altro sguardo su di noi. (...)
LA COMMON DECENSE
La via della decrescita è dunque prima di tutto una scelta. (...) È, in ogni caso, una via d’uscita dall’enorme decadenza generata dalla società della crescita. Una via d’uscita per recuperare la stima di se stessi. È la via per ricostruire una società decente. Una società decente, dice il saggio, è una società che non umilia i suoi membri. È una società che non produce rifiuti.
La via della decrescita è anche la common decense di George Orwell. La decenza comune significa avere ritegno, essere attenti, essere capaci di avere vergogna per quello che viene fatto al mondo e alle persone. «Essere svergognati - dice Bernard Stiegler - significa essere diventati incapaci di avere vergogna». La società della crescita è un mondo svergognato, un mondo in cui regna il disprezzo. E il desiderio di sfuggire al disprezzo è una aspirazione universale (forse la sola veramente universale) che si realizza soltanto nelle società decenti. L’assenza di ritegno, la mancanza di attenzione equivalgono all’assenza della decenza comune definita da Orwell. Un mondo decente forse non è un mondo di abbondanza materiale, ma è un mondo senza miserabili e senza brutture. (...)
Quando diciamo che la decrescita è un progetto politico, intendiamo che è anche un’etica, perché per noi, come per Aristotele, la politica non è concepibile senza un’etica, e viceversa, anche se è opportuno non confondere i due piani. Una politica che fosse soltanto un’etica sarebbe impotente o terroristica, ma una politica senza etica (come quella che viviamo soprattutto a partire dalla svolta degli anni novanta, dal grande balzo all’indietro neoliberale) vede il trionfo della banalità del male. (...) La via della decrescita è anche quella dell’emancipazione e della conquista dell’autonomia. È la ricerca della libertà vera e non della sua caricatura, quella dell’edonismo sfrenato e senza regole proposta dalla pubblicità e dal marketing e promossa dal nuovo spirito del capitalismo, falsamente gioioso e di fatto mortifero. (...) La via della decrescita è un’uscita di emergenza dal vicolo cieco dell’immondializzazione. La via della crescita è un esilio. È la traversata del deserto verso la terra promessa, ma è anche un’oasi nel deserto della crescita. «La rivoluzione - ammonisce Jérôme Baschet - non ha senso se non si concepisce al tempo stesso come una festa, se si priva di quelle occasioni così importanti come un ballo o uno scoppio di risa... È vano voler combattere l’alienazione in forme alienate... Bisogna ammettere l’impossibilità di condurre una vera lotta per l’umanità senza cominciare a percepire nel processo stesso di questa lotta la verità dell’umanità alla quale si aspira, senza riconoscere il diritto al piacere e la necessità di una poesia che non è altro che il nome dato a un’esistenza veramente degna dell’uomo».(...)
La decrescita è un’arte di vivere. Un’arte di vivere bene, in accordo con il mondo. L’obiettore di crescita è anche un artista. Qualcuno per il quale il godimento estetico è una parte importante della sua gioia di vivere. (...) Fare della propria vita un’opera d’arte non è l’obiettivo, ma uno dei risultati. La via della decrescita è un’ascesi. Limitandosi all’aspetto curativo e alla lotta contro la tossicodipendenza da consumismo, si può riprendere l’idea di Ivan Illich del «tecnodigiuno». La decrescita è un esercizio di emancipazione dalle protesi tecniche, una liberazione dalla servitù volontaria e un allenamento all’autonomia.
La via della decrescita è una conversione di se stessi e degli altri. La conversione richiesta per realizzare la trasformazione sociale necessaria e desiderabile presuppone che si crei un atteggiamento di accoglienza e di apertura a questo cambiamento. Questa educazione è, al tempo stesso e indissolubilmente, sapere ed etica, resistenza e dissidenza. (...)
La via della decrescita è riconquista della realtà e della terra che ne è il principio. Si tratta di abitare la terra come un territorio, un luogo di complicità e di reciprocità. Di ritrovare la nostra intimità con una dimensione originaria. «Oggi una linea di orizzonte tecnica - scrive in modo ispirato Xavier Bonnaud - separa l’uomo dalla fauna e dalla flora. Questi elementi che l’uomo ha allontanato, indebolito e canalizzato non producono più in lui quelle relazioni affettive profonde che derivavano da un contatto diretto». (...)
La via della decrescita è quella della libera critica. È quella dell’autolimitazione e non dello scatenamento senza freni delle passioni tristi. La decrescita vuole riprendere il programma di emancipazione politica della modernità, affrontando le difficoltà che comporta la sua realizzazione. L’esperienza autenticamente democratica instaura un’esperienza di trascendenza dell’uomo nell’uomo che permette di uscire dalle aporie dell’egualitarismo.
Come dice il filosofo belga Robert Legros: «Riconoscere una limitazione dei poteri dell’uomo che non sia una autolimitazione, significa chiaramente ammettere una eteronomia al centro dell’autonomia. Interpretare questa limitazione come una norma inscritta nell’umanità dell’uomo, e non come una norma di origine religiosa, significa tentare di cogliere il senso di una eteronomia propriamente democratica». Se la decrescita e il progetto di costruzione di una società autonoma realizzano il sogno di emancipazione dei Lumi e della modernità, non lo fanno attraverso uno svincolamento dal legame con la natura e dal radicamento nella storia, ma al contrario riconoscendo la doppia eredità della nostra naturalità e della nostra storicità. Bisogna lottare contro l’illimitatezza dell’individuo e del suo rapporto con la natura che abbiamo preteso di creare.La via della decrescita è questa lotta. La via della decrescita è una emancipazione dalla religione della crescita. Richiede dunque necessariamente anche un «decredere». Bisogna abolire la fede nell’economia, rinunciare al rituale del consumo e al culto del denaro.
Per i teologi Alex Zanotelli, don Achille Rossi, don Luigi Ciotti e Raimon Panikkar, come per Ivan Illich o Jacques Ellul, la società della crescita poggia su una struttura di peccato. Contrariamente alla formula sventurata dell’enciclica Populorium progressio, lo sviluppo non è il nuovo nome della pace ma quello della guerra, guerra per il petrolio o per le risorse naturali in via di esaurimento. Nella società della crescita non ci sarà mai più né pace né giustizia. Al contrario, una società della decrescita riporterà al proprio centro la pace e la giustizia. Non si vuole cadere nell’illusione di una mitica società perfetta in cui il male sarebbe sradicato definitivamente, ma inventare una società dinamica che affronta le sue inevitabili imperfezioni e contraddizioni dandosi come orizzonte il bene comune anziché l’avidità sfrenata. La via della decrescita non è una religione né un’antireligione, è una saggezza.
Per gli obiettori di crescita la ricerca della via è un dovere, ma non è un imperativo categorico di tipo kantiano, anche se noi facciamo nostro l’imperativo kantiano così come riformulato da Hans Jonas: «Agisci in modo che gli effetti della tua azione siano compatibili con la permanenza di una vita autenticamente umana sulla terra».
© Come si esce dalla società dei consumi. Corsi e percorsi della decrescita, Bollati Boringhieri editore Torino 2011 Traduzione di Fabrizio Grillenzoni
-
-
> MATEMATICA E CIVILTA’: UNA CRISI EPOCALE. --- L’UNO E I MOLTI, NEL SEGNO DELL’ILLUMINISMO - KANTIANO! "Un’eredità plurale" (di Remo Cesarani).23 febbraio 2011, di Federico La Sala
Un’eredità plurale
L’attaccamento alle radici comporta inevitabili conflitti. Anziché affannarsi a cercare dubbie identità, è più utile rifarsi alle lezioni di Jürgen Habermas e di Denis de Rougemont che da prospettive differenti prefigurano comunità caratterizzate da valori di inclusione e solidarietà.
di Remo Ceserani (il manifesto, 23 febbraio 2011)
Tutti si affannano, in questi giorni, e riempiono le pagine dei giornali, dei siti web, dei blog, e delle trasmissioni televisive, per discutere di identità: l’identità italiana, le radici cristiane dell’Italia o dell’Europa, l’identità padana (del tutto immaginaria e composita), e così via. La parola «identità», usata a proposito e a sproposito, compare sempre più spesso nei discorsi degli storici e dei giornalisti italiani, con insistito riferimento, in questi ultimi tempi, all’identità italiana (un’identità, come è noto, abbastanza incerta e traballante e prodotta con qualche fatica attraverso le vicende del Risorgimento, del Fascismo e della Resistenza). Tutti sappiamo che l’idea di una identità forte, sia delle singole persone (gli imprenditori, i costruttori del proprio destino, i protagonisti della propria vita), sia delle singole comunità (i gruppi sociali, le classi, le nazioni) sono un prodotto tipico della modernità, basato su forti investimenti ideologici e su vere e proprie costruzioni di sé con tutti gli strumenti offerti dalla mitologia (le origini, le radici) e dall’immaginario (la storia, la bandiera, gli inni, le date fatidiche, sia delle vittorie sia persino in certi casi, delle sconfitte, come è avvenuto per l’identità serba in seguito alla vittoria turca nella Piana dei Merli, nel Kosovo, il 15 giugno 1389, giorno di San Vito).
Individui in movimento
Forse è il caso di dirci, sommessamente, che si corrono grossi rischi, e si cade in troppe rigidità ideologiche, quando si parla di identità. L’attaccamento alle radici, siano esse etniche, culturali o, peggio ancora, religiose, comporta un’inevitabile conseguenza di conflitti. La difesa della propria identità prevede un confronto, e spesso un contrasto (anche violento) con le identità altrui. Il panorama mondiale è ancor oggi pieno di conflitti che nascono proprio dalla rivendicazione delle proprie radici e dallo scontro fra identità diverse. E la storia offre esempi infiniti di guerre tribali, interetniche, civili, nazionali, mondiali, nate da simili rivendicazioni.
Oggi in teoria saremmo in un mondo, quello della globalizzazione o della modernità liquida, in cui gli individui si muovono sempre più rapidamente e attraversano molti confini: sono immigrati che lasciano i paesi poveri o i regimi polizieschi per andare a vivere in società più aperte e più ricche di opportunità di lavoro. Sono giovani che hanno ottenuto una formazione nelle università e in centri di ricerca del proprio paese e, per sfuggire a strutture chiuse e corporative, o per semplice desiderio di ampliare conoscenze ed esperienze, vanno a operare nei centri di ricerca o nei laboratori di altri paesi. Sono persone che si trapiantano per necessità o per gusto della novità e dell’avventura. Sono i protagonisti della mobilità sociale. Sono coppie che si formano dopo l’incontro fra individui (uomini o donne) appartenenti a culture diverse, che vanno a vivere presso uno di loro oppure si spostano entrambi in un paese terzo.
Nel segno dell’illuminismo
Se esaminiamo questo problema dal punto di vista della teoria sociale, non possiamo che contrapporre all’idea di «identità» (ossia l’attaccamento più o meno volontario alle proprie radici e alla propria comunità di origine, la disponibilità a rafforzarla e difenderla fino al sacrificio - «pro patria mori»), l’idea di «appartenenza», ossia la libera scelta della comunità in cui vivere e disponibilità a rafforzarla e difenderla, con juicio e possibilmente con armi pacifiche. È stato chiarissimo in proposito il filosofo tedesco Jürgen Habermas, che ne ha parlato al tempo della discussione sulla costituzione europea e dello scontro con chi insisteva - fra questi non solo i prelatidel Vaticano ma anche Fini, se ben ricordate - sulla necessità di inserire nel testo la rivendicazione dell’identità cristiana dell’Europa.
Habermas respingeva qualsiasi idea tradizionale di nazione come «una comunità del destino plasmata da una comune eredità, una lingua e una storia comuni», e dichiarava di concepire piuttosto le nostre nazioni moderne come comunità di cittadini: «una comunità civica, anziché etnica», la cui identità collettiva «non esiste indipendentemente o antecedentemente al processo democratico da cui scaturisce» (Tempo di passaggi, Milano, Feltrinelli, 2004, ma vedi anche Ach Europa!. Kleine politische Schriften XI, Frankfurt, Suhrkamp). Rifacendosi all’idea illuministica degli Stati moderni come formazioni storiche fondate su un contratto costituzionale, procedure democratiche, condivisione d’interessi economici, valori culturali, interpretazioni del passato e sviluppo di una «sfera pubblica», Habermas concepisce l’Europa come una comunità specifica di cittadini (citoyen) caratterizzata dalla presenza condivisa di valori come la solidarietà, l’orientamento verso il sociale, l’inclusione politica ed economica. Questo passaggio del discorso di Habermas mi sembra di grande importanza: sarebbe bene che chi può scegliere la comunità alla quale aderire, ammesso che la possibilità di scelta sia reale (e temo che, pur con tutta la mobilità sociale del mondo globalizzato, quelli che possono scegliere non siano molti), preferisse una comunità caratterizzata da valori condivisi come «la solidarietà, l’orientamento verso il sociale, l’inclusione politica ed economica». Per fare qualche esempio dal mondo occidentale dopo la grande crisi: molti paesi europei sembrano poco inclini all’inclusione politica ed economica degli immigrati; l’Inghilterra e gli Stati Uniti, che tendono a cancellare il welfare, sembrano poco orientati verso la solidarietà e il sociale.
Il federalista Gioberti
Se poi esaminiamo il problema dal punto di vista della storia (di gran moda ai nostri giorni, in cui abbiamo delegato al bravissimo Benigni di tentare la ricostruzione, con l’aiuto di Aldo Cazzullo, delle vicende del Risorgimento - ma forse avrebbe fatto meglio a chiedere l’aiuto anche di Alberto Mario Banti), credo doveroso riconoscere che il problema dell’identità italiana sia un vero ginepraio. Tutti noi, nati nell’una o nell’altra regione italiana, abbiamo problemi non piccoli a risalire all’indietro nella storia e a identificare le nostre origini e identità. Cosa sono io, nato in Lombardia? Di eredità celtica, o germanico-longobarda, o villanoviana, etrusca, latina, romana? O addirittura pelasgica, come voleva Gioberti, uno dei padri della patria di cui si parla poco in questi giorni, il quale nel 1846 si fece sostenitore di un’Italia unificata con il consenso papale e nel 1848 si proclamò federalista? Sentite cosa scriveva nel Primato: «Il genio proprio degli Italiani nelle cose civili risulta da due componenti, l’uno dei quali è naturale, antico, pelasgico, dorico, etrusco, latino, romano, e s’attiene alla stirpe e alle abitudini primitive di essa; l’altro è sovrannaturale, moderno cristiano, cattolico, guelfo, e proviene dalle credenze e instituzioni radicate, mediante un uso di ben quindici secoli e tornate in seconda natura agli abitanti della penisola. Questi due elementi, che sono entrambi nostrani, ma il primo dei quali è specialmente civile e laicale, il secondo religioso e ieratico, insieme armonizzano, giacché essendo logicamente simultanei e cronologicamente successivi, ma con assidua vicenda, l’uno compie l’altro, e corrispondono ai due grandi periodi della nostra istoria prima e dopo di Cristo, e alle due instituzioni italiane più forti e mirabili (alle quali credo che niun’altra si possa paragonare) cioè all’imperio latino nato dalla civiltà etrusco pelasgica, e alla dittatura civile del Papa nel medio evo, procreata dal Cristianesimo».
Tre città-simbolo
Vorrei, a tutti quanti si tormentano sulla questione dell’identità italiana, e ancor più su quella dell’identità europea, ricordare le parole di un grande intellettuale ginevrino, Denis De Rougemont, calviniano, figlio di un pastore, ma anche spirito libero e coraggiosamente radicale, che negli ultimi anni della sua vita, dopo la formazione parigina (il cui frutto fu un libro curioso e controverso: L’amore e l’occidente, 1939) e un lungo soggiorno americano, da Ginevra si spese con grande energia in favore dell’Europa, proponendo uno Stato federale basato sul modello della Svizzera (Écrits sur l’Europe, a cura di Christophe Calame, Parigi 1994). De Rougemont insiste sullediversità delle tante componenti che formano l’Europa e sul loro ruolo fecondo (lo stesso, a maggior ragione, dovremmo dire dell’Italia): «la diversità delle tradizioni, delle lingue, dei partiti, delle nazioni e persino delle religioni, è una condizione fondamentale della creatività e dello spirito d’invenzione» propri dell’Europa.
Nella ricerca delle memorie condivise, De Rougemont mette in campo le tre città-simbolo della grande tradizione: Atene, Gerusalemme, Roma, e poi numerose culture: l’Oriente, la Grecia, il Cristianesimo, i Celti, i Germani, gli Arabi, gli Scandinavi, gli Slavi. Egli ricorda per esempio l’apporto celtico del gusto per l’avventura, per la dismisura e per la potenzialità trasfigurante del sacrificio e della sconfitta, oppure l’apporto germanico e celtico dell’ideologia cavalleresca e della fedeltà di appartenenza al clan e al ceto nobiliare, oppure ancora l’apporto occitanico della concezione cortese della vita e dell’amore, arricchita di elementi della gnosi e dell’erotismo arabo. Ma ricorda anche altri elementi, che spiegano l’insieme complesso e pieno di contraddizioni delle identità europee: 1) la molteplicità delle lingue ma anche le loro profonde e nascoste affinità, dovute all’eredità indoeuropea, che accomuna quasi tutte le lingue antiche e moderne del continente (ricorda per esempio la presenza in molti paesi dei derivati dei termini dubron e dour che in celtico e in brettone armoricano significavano «acqua», come dimostrano i nomi dei fiumi Douro in Spagna, Drance e Thur in Svizzera, Dordogne, Durance, Drôme e Dore in Francia, le due Dore in Italia, la Dordrecht in Olanda e venti altri fiumi europei); 2) la lunga tradizione di organizzazioni statali e burocratiche forti, ereditate dall’opera di romanizzazione, che ha portato gli Europei a costruire stati-nazione molto accentrati e autoreferenziali e, sottolinea De Rougemont, a non saper concepire Dio o la vita spirituale al di fuori dei quadri istituzionali delle Chiese; 3) la concezione della persona umana fortemente autonoma e impegnata a seguire una propria vocazione indipendente, ma capace di contribuire alla fondazione di valori condivisi della comunità (eredità greco-cristiana colorata di valori germanici e celtici); 4) lo spirito critico e la propensione a liberarsi dall’impalcatura del sacro e dal culto dei morti, dai miti tribali, dalle credenze religiose nate dalla paura (che De Rougemont considera una eredità propriamente evangelica); 5) la tendenza, purtroppo molto diffusa, a lasciarsi condizionare dai legami pesanti con la materialità (e quindi a essere meno distaccati e liberi rispetto, per esempio, ai popoli influenzati dall’induismo o dal buddismo); 6) la tendenza, inoltre, a lasciarsi attrarre dall’astrazione (e quindi essere meno capaci di comunicare con le proprie forze vitali dei popoli africani influenzati dall’animismo).
Appartenenza e egoismo
Mi pare un quadro straordinariamente efficace delle nostre tante diversità e un programma convincente in favore di un’Italia, e di un’Europa, non delle identità, ma delle differenze e delle appartenenze. De Rougemont aveva in mente la Svizzera: un paese in cui convivono tre religioni e quattro lingue, orgoglioso della sua indipendenza, delle sue istituzioni politiche, unito non da ragioni di identità etnica, linguistica o religiosa, ma da peculiari, rispettabilissime, tradizioni storiche (ma anche, si deve aggiungere, da non poche ragioni di convenienza e interessi economicomateriali, e da una solidarietà un po’ chiusa su di sé e corretta da un qualche egoismo - come dimostra il recente affacciarsi sulla scena politica di un movimento xenofobo come il Ppd di Christof Blocher).
Tutto considerato, mi pare che la lezione di De Rougemont, così come quella di Habermas, potrebbe essere estremamente salutare in un’Italia come è quella in cui viviamo, estremamente confusa e distratta.